這應該是最後一天寫 Heap
從 buildMaxHeap 到 HeapSort
明天就會從更複雜（？）的樹開始繼續往下

buildMaxHeap

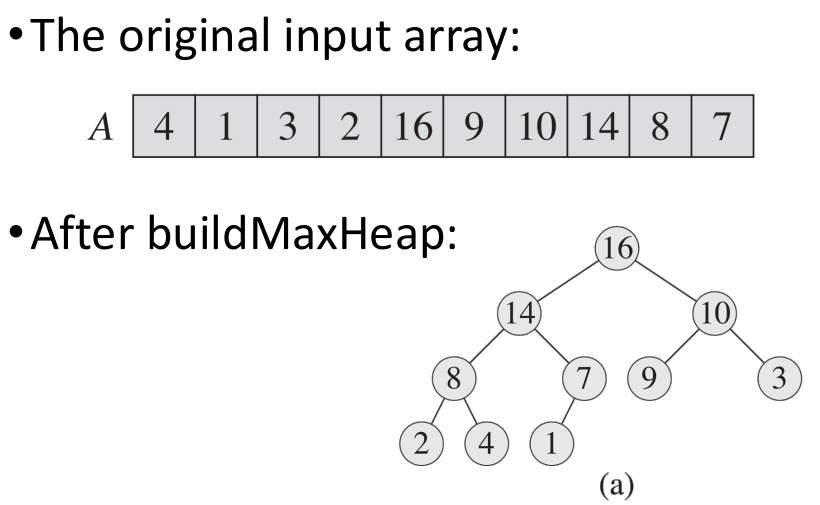
從一組給定的數組建構 Max Heap，並從昨天的 maxHeapify 程式，建構一個 nearly complete binary tree

buildMaxHeap(A, N){
    for(i =parent(N − 1); i ≥ 0; i--){
        maxHeapify(A, N, i);
    }
}

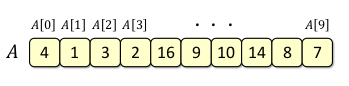
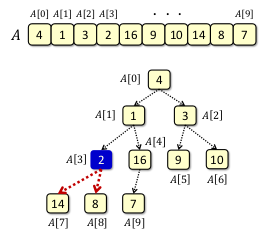
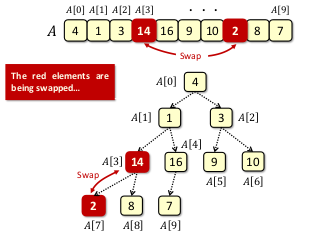
經過好幾次的對調之後，便完成 buildMaxHeap 的工作

時間複雜度

buildMaxHeap 的時間複雜度為 O(n)，n 表示 Array 中有幾個元素

首先，假設 Heap 高度為 h，如圖：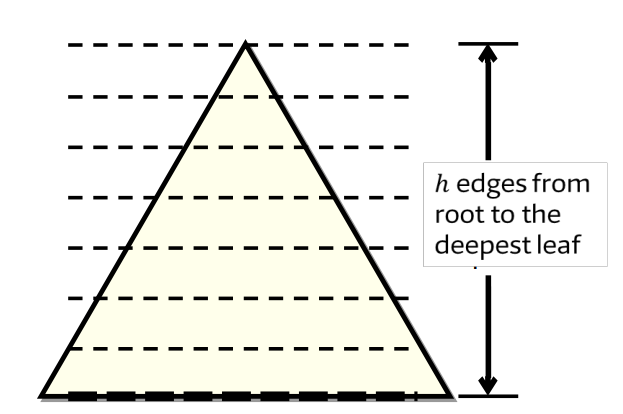

N = 2^(h+1) - 1

• 最底層共 (N+1)/2 的葉子並不需要進行 maxHeapify
• 倒數第二層每次交換最少需要進行一次的 swap，共 (N+1)/4 × 1 個 swap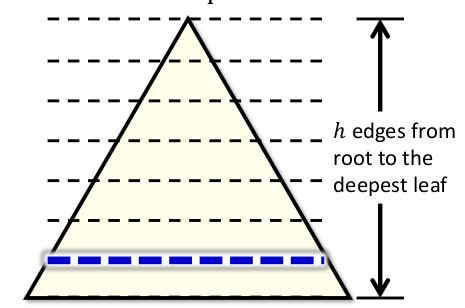
  
• 再更往上一層每次交換最少需要進行兩次的 swap，共需要 (N+1)/8 × 2 個 swap
• 再更往上一層每次交換最少需要進行三次的 swap，共需要 (N+1)/16 × 3 個 swap
• 到 root 時，共需 1 × h swaps

經過上面的步驟：(N+1)/4 × 1 -> (N+1)/8 × 2 -> (N+1)/16 × 3 -> ... -> lg(N+1) - 1
此時：

heapSort

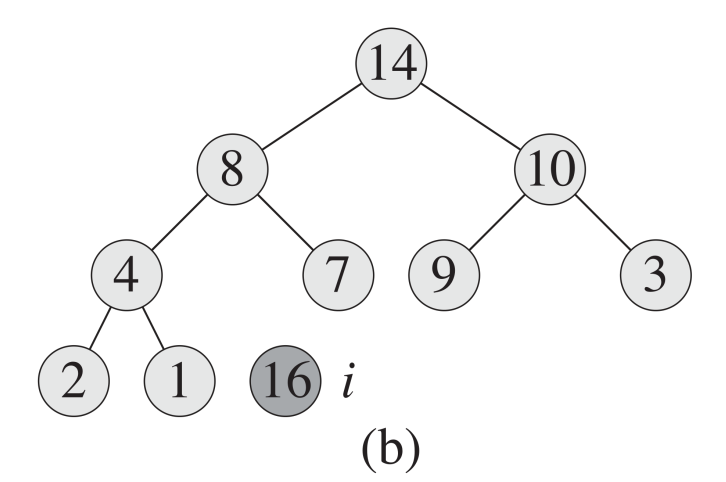
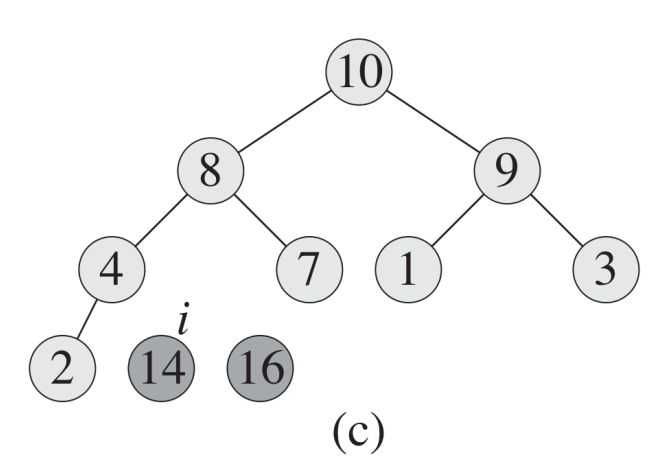
heapSort 的中心思維就是一直從 heap 中取出最大值，直到 heap 為空

heapSort(A, N){
    buildMaxHeap(A, N);
    for(i = N − 1; i ≥ 0; i − −){
    
        // 將最大值放入 array 尾端
        Exchange A[0] and A[i];
        
        // heap 的 size 減少 1
        maxHeapify(A, --N, 0);
    }
}

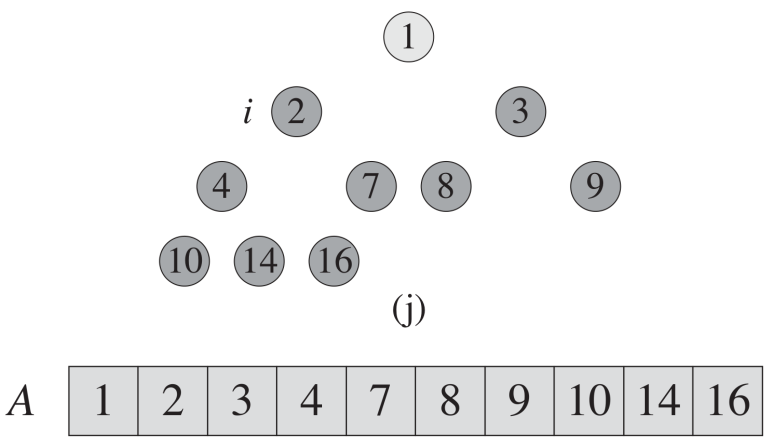
Source: 我們教授ㄉ講義，推推！